November 16, 2005
“In anxious and uncertain times like ours, when it is difficult to find pleasure in humanity and the course of human affairs, it is particularly consoling to think of the serene greatness of a Kepler. Kepler lived in an age in which the reign of law in nature was by no means an accepted certainty. How great must his faith in a uniform law have been, to have given him the strength to devote ten years of hard and patient work to the empirical investigation of the movement of the planets and the mathematical laws of that movement, entirely on his own, supported by no one and understood by very few! If we would honor his memory worthily, we must get as clear a picture as we can of his problem and the stages of its solution.”
These were the words that Albert Einstein published in the Frankfurter Allgemeine Zeitung on November 9, 1930, for the commemoration of the 300th anniversary of Kepler’s death. Now, seventy-five years later, these words still ring true, and they provide a suitable vantage-point from which to investigate what is as relevant today as it was then: the connection between epistemology and the general condition of mankind.
There is an ironical benefit in exploring this connection from the perspective of Einstein’s view of Kepler. Though Einstein recognized the importance of the connection between the state of science and the state of society, he failed to grasp its deeper epistemological implications as Kepler had. Yet the problems that Einstein faced persist unresolved to this day. Thus, by viewing Kepler from Einstein’s eyes and Einstein from Kepler’s, we can apply Kepler’s approach to the problems Einstein identified.
The world in November 1930 was indeed an “anxious and uncertain time”, as Einstein remarked. A global depression was deepening, while the London-centered international synarchist financiers were rapidly consolidating fascist control over the governments of Europe and Japan, with the intention of striking at the United States, and establishing a global, neo-feudalist, fascist world empire. As Lyndon H. LaRouche has elaborated in many locations, most recently in Globalism Is The New Imperialism, this crisis was rooted in the British imperialist reaction to the defeat of their puppet Confederate States of America, and the subsequent spread of the American System to continental Europe and significant parts of Asia by Abraham Lincoln’s allies. Adopting a strategy similar to that used by their ancient Persian and Babylonian ancestors after failing to militarily defeat Athens and her allies in the fifth century B.C., the British-centered imperialists switched from a primarily military strategy to destroy the American system, to one of seeking to subvert the cultural dominance of the scientific principles on which that system was based.
These efforts had their greatest effect in Europe. In the aftermath of the American Revolution, the British had orchestrated the Jacobin Revolution, the Napoleonic dictatorship and the 1815 Congress of Vienna, which had spread a wave of enforced cultural pessimism intended to demoralize Europe’s American allies, and to destroy the optimism generated by the success of the American cause. With the resurgence of pro-American system reforms on the European continent in the second half of the nineteenth century, the oligarchy accelerated the spread of this cultural pessimism, typified by the increasing popular acceptance of such mind-deadening cultural movements as the existentialism of Friedrich Nietzsche and Richard Wagner’s cult-operas.
In science, such cultural pessimism was expressed by attacks on the Leibnizian tradition of Gauss, Dirichlet, Riemann et al., exemplified by the swindles of Napoleon’s favorite mathematician, Lagrange, the popular acceptance of British-centered empiricism, associated with Maxwell, Lord Kelvin, et al., and the reassertion of Cartesian formalism by Cauchy. By Einstein’s time, this degeneration in science manifested itself most prominently in the more radical forms of irrationality expressed by the Copenhagen interpretation of quantum phenomena.
Though Einstein had stubbornly resisted the introduction of such radical positivism into science, he had been politically targeted by the liberal-imperialist wing of these London-based synarchists. Playing on his political naivete and his vulnerability to cultural pessimism, they sought, sometimes successfully and sometimes not, to manipulate a politically unsophisticated Einstein for their own ends. As a result, Einstein was confused about the true cause of the global anxiety to which he referred, and mystified as to its solution. Nevertheless, he recognized that the degeneration of society that he was witnessing coincided with a similar degeneration in science, of which he had a more clear, albeit incomplete, conception.
It is not surprising that Einstein would find a kindred spirit in Kepler, whose understanding of the problems confronting science and society was much deeper than his own. In Kepler’s time, irrationality also dominated European society, despite the previously higher level of sanity that had been initiated by the circles associated with Nicholas of Cusa, nearly two centuries earlier. At that time, these humanists had seized the opportunity afforded them by the collapse of the feudalist Bardi and Peruzzi banking houses, to assert, as a principle in society, the Socratic concept of man. Cusa insisted, as Socrates and Plato had, that cognition, though unique to human beings in a self-conscious form, reflects a general characteristic of the Universe itself. Thus, contrary to the Aristotelean dogma that had dominated Europe since the collapse of Greek society in the centuries following the Peloponnesian Wars, Cusa understood, like Socrates and Plato, that the material universe is not indifferent to human thought, but that man, through his power to discover universal physical principles, is integral to the self-development of the Universe as a whole.
Cusa went further, specifying that the organization of human affairs must be based on a recognition of the role of the human mind in the physical world. His circles were able to establish a foothold in society, exemplified by the achievements in science and art of Brunelleschi, DaVinci, Pacioli, and the improvements in society created by the establishment of the first nation-states in Louis XI’s France and Henry VII’s England.
In reaction, the Venetian-centered financiers, heirs to the traditions of Imperial Rome, sought desperately to re-establish feudal control over Europe by weakening the optimistic concept of man that had taken hold in the Renaissance. Beginning with the 1492 Spanish Inquisition, Venice and her allies unleashed religious warfare throughout Europe aimed at reintroducing a fundamentally irrational view of man and the universe as a dominant feature of European culture. By the end of Kepler’s life, this horror was erupting into the final orgy of insanity which is today called the Thirty Years War.
But Kepler understood that the insanity on the ground reflected an irrational view of heaven. Astronomy in Kepler’s time had degenerated from the search for universal physical principles that had characterized the Egyptian-Pythagorean science of Sphaerics and reverted back to the Babylonian-Persian model, which held that Man was incapable of discovering anything truthful about the nature of the physical world, and consequently, must accept whatever irrational dogma the reigning authorities preferred. This view, which shackled science to sophistry, was designed to impute to the heavens a justification for oligarchical-imperial forms of society.
Invoking Eratosthenes’ description of the Delian problem, Kepler, like Plato, implored his contemporaries to recognize that their false view of the planets reflected an equally false view of themselves. The acceptance, by scientists and society at large, of Aristotelean doctrines, was the cause of the political and social collapse they were experiencing. Kepler, an avowed follower of Cusa, insisted that the governing principles of the universe were congruent with the ability of the human mind to discover those principles. Further, the existence of that ability was itself an indication that the characteristics of human creativity were characteristics of the Universe as a whole. As he wrote in his Optics:
Anyone who ponders this carefully will find (if he will refuse to have recourse to faith in holy scripture) both that there is a God, founder of all nature, and that in the very mechanics of it he had care of the humans that were to come. For this theater of the world is so ordered that there exist in it suitable signs by which human minds, likenesses of God, are not only invited to study the divine works, from which they may evaluate the founder’s goodness, but also are assisted in inquiring more deeply.
Kepler rejected the common error of Ptolemy, Copernicus and Brahe, who remained faithful to Aristotle’s dictat that the planetary orbits must be perfectly uniform circles. Instead, Kepler adopted Cusa’s view, that change was a beneficent characteristic of both Man and the physical world, and thus, the non-uniform elliptical orbit more perfectly expressed the self-perfectability of the Universe, than the mathematically perfect circles. In demonstrating from the experimentally determined evidence that the planetary orbits were indeed non-uniform and determining the principles governing that motion, Kepler was demonstrating, contrary to Aristotle, that not only is the physical universe characterized by change, but that the human mind is capable of knowing it.
For Kepler, the planet, as a material object, does not exist in a purely material world, and its orbit is not governed purely by material principles. Rather, the planet’s historical and future trajectory is a pathway through a universe in which the principles of physics, life and cognition are each and all acting everywhere and at all times. Thus, the principles governing planetary motion not only to guide the planet, they guide the human mind toward their discovery. As Kepler emphasized, Mind is a principle in the material world.
By demonstrating that he could discover and communicate the true principles governing planetary motion, Kepler was not only advancing astronomy, he was asserting an optimistic concept of Man and nature in the face of a prevailing opinion that had been induced to accept irrationality and arbitrariness in both science and human affairs.
In Einstein’s time this cultural irrationality had once again begun to dominate science. By the end of the nineteenth century, an increasing amount of experimental evidence, such as the photoelectric effect and Planck’s discovery of the quantization of light and heat, indicated the existence of a fundamental change in the characteristics of physical action between the macroscopic and microscopic domains. These discoveries were consistent with the earlier work of Gauss, Fresnel, Riemann, Weber, et al. who, extending Leibniz’s method of the infinitesimal calculus, had discovered microscopic principles from their experimentally determined macroscopic effects. This led Riemann, in his habilitation dissertation, to insist that it was scientifically unsound to assume that the characteristics of physical action in the macroscopic domain could be linearly extended into the very large and very small. Instead, Riemann insisted, science must develop a dynamic notion of physical geometry that reflected the potential for non-linear change between these domains of action.
As Riemann stated:
Knowledge of the causal connection of phenomena is based essentially upon the precision with which we follow them down into the infinitely small....In the natural sciences, however, where simple fundamental concepts are still lacking for such syntheses, one pursues phenomenon into the spatially small, in order to perceive causal connections, just as far as the microscope permits. Questions concerning spatial relations of measure in the indefinitely small are therefore not useless.
In reaction, the British-empiricists tried to revive Kant and Euclid, most notably through the work of James Clerk Maxwell, who famously rejected Riemann’s approach to physics, in favor of the neo-Euclidean doctrine which excluded “any geometries other than our own”. Thus, when the relationship between the observed macroscopic effects of electro-magnetism were considered in light of the growing body of experimental evidence indicating a change in physical characteristic in the microscopic domain, Riemann’s guidance proved to be essential, which Einstein recognized.
Among Einstein’s contemporaries, however, there was a growing popularity among scientists to “explain” these phenomena by statistical methods, similar to those used by Ptolemy, Copernicus and Brahe. These efforts were led by Niels Bohr, his protege, Werner Heisenberg, and Heisenberg’s first teacher, Max Born.
This positivist view insisted that because they knew of no mathematical description of these phenomena other than statistical methods, the universe itself must be fundamentally random. In other words, Bohr, Heisenberg and Born et al. argued, not that they merely didn’t know the principles on which these phenomena were based, but that no such principles existed. Since no principles existed, none could be discovered.
Born summarized his view of the dispute in the published collection of his correspondence with Einstein:
The basic reason for the dispute between us on the validity of statistical laws was as follows. Einstein was firmly convinced that physics can supply su with knowledge of the objectively existing world. Together with many other physicists I have been gradually converted, as a result of experiences in the field of atomic quantum phenomena, to the point of view that this is not so. At any given moment, our knowledge of the objective world is only a crude approximation from which, by applying certain rules such as the probability laws of quantum mechanics, we can predict unknown (e.g. future) conditions.
It is important to emphasize that this view, known generally as the Copenhagen interpretation of quantum phenomena, like Ptolemy’s astronomy, was not science. It was a post hoc cult-like belief reflecting, and ultimately used to justify, the prevalent existentialism associated with the drive to establish fascist forms of oligarchical control over the world. In the tradition of the Empires of Babylon, Persia and Rome, the London-based imperialists intention was to undermine the successful spread of the cultural optimism associated with the American system returning to the era of wizards and serfs.
The axiomatic foundations of the Copenhagen school have since become so entrenched in popular opinion, that they are accepted as doctrine even by people who know nothing of physics as exemplified by the widespread acceptance of the belief that the Mandevillian doctrines of free trade reflects the, “natural order of things”.
Einstein, Planck and a handful of others rejected this radical positivism, stubbornly defending causality in science throughout the early decades of the twentieth century. In September 1926 Einstein stated his view clearly to Born:
Quantum mechanics is certainly imposing. But an inner voice tells me that it is not yet the real thing. The theory says a lot, but does not really bring us any closer to the secret of the ‘old one’. I, at any rate, am convinced that He is not playing at dice. Waves in 3-dimensional space, whose velocity is regulated by potential energy (for example, rubber bands)...I am working very hard at deducing the equations of motion of material points regarded as singularities, given the differential equation of general relativity.
Writing to Born years later, in September 1944, Einstein summed up the view he had continued to express:
We have become Antipodean in our scientific expectations. You believe in the God who plays dice, and I in complete law and order in a world which objectively exists, and which I, in a wildly speculative way am trying to capture. I firmly believe, but I hope that someone will discover a more realistic way, or rather a more tangible basis than it has been my lot to find. Even the great initial success of the quantum theory does not make me believe in the fundamental dice-game, although I am well aware that our younger colleagues interpret this as a consequence of senility. No doubt the day will come when we will see whose instinctive attitude was the correct one.
In September 1950, after his association with Kurt Goedel had improved his historical and epistemological knowledge, Einstein wrote Born saying:
I see from the last paragraph of your letter that you, too, take the quantum theoretical description as incomplete (referring to an ensemble). But you are after all convinced that no (complete) laws exist for a complete description, according to the positivistic maxim esse est percipi. Well, this is a programmatic attitude, not knowledge. This is where our attitudes really differ. For the time being, I am alone in my views–as Leibniz was with respect to the absolute space of Newton’s theory. There now, I’ve paraded my old hobby-horse once again. But it is your own fault, because you provoked me.
But though Einstein remained stubborn in his resistance to the radical positivism of the Copenhagen interpretation, and he spent most of his efforts trying to develop a concept that would replace it, he was unable to succeed for two related reasons. One, unlike Kepler and Leibniz, he had been unable to completely rise above the prevailing cultural pessimism reflected in the degeneration of science and society, and two, he failed to recognize, as his contemporary Vernadsky had indicated, that the questions posed by experimental evidence of quantum phenomena could not be answered in the domain of mathematical physics. In referring to an “objective world” in his rejection of the Copenhagen interpretation, Einstein was tacitly accepting the Aristotelean sophistry that the world of thought and the world of physics were separate. Rather, these questions can only be addressed when physical phenomena are recognized, as Kepler did, as observed effects within a universe in which physics, life, and thought interact in what Riemann called a multiply-connected manifold.
Today, the only competent way to approach these questions is from the standpoint of the science of physical economy, as that science has been developed by Lyndon H. LaRouche. That approach requires an understanding of what Gauss and Riemann identified as the hypergeometric domain.
The Universe From the Inside
To begin to get an understanding of what emerged as a hypergeometric conception of the Universe , we can start by examining the problem that Einstein identified in his 1930 commemoration of Kepler: the determination of the orbit of the Earth. This posed a significant challenge because it meant determining the orbit of the Earth while on the Earth, or more generally, determining the motions of the solar system while moving in the solar system.
Kepler understood that any particular scientific investigation, such as the determination of the orbit of Mars, is actually an investigation of the Universe as a whole, not of a particular phenomenon. Any attempt to reduce the problem to a small set of particulars would be nothing more than sophistry. This more general problem can be stated: how to determine the eternal dynamic nature of the Universe itself, from within the temporal unfolding of that eternal dynamic?
As Einstein wrote in his 1930 essay:
Copernicus had opened the eyes of the most intelligent to the fact that the best way to get a clear grasp of the apparent movements of the planets in the heavens was by regarding them as movements around the Sun conceived as stationary. If the planets moved uniformly in a circle around he Sun, it would have been comparatively easy to discover how these movements must look from the earth,. Since, however, the phenomena to be dealt with were much more complicated than that, the task was a far harder one. The first thing to be done was to determine these movements empirically from the observations of Tycho Brahe. Only then did it become possible to think about discovering the general laws which these movements satisfy.
To grasp how difficult a business it was even to find out about the actual rotating movements, one has to realize the following. One can never see where a planet really is at any given moment, but only in what direction it can be seen just then from the Earth, which is itself moving in an unknown manner around the Sun. The difficulties thus seemed practically unsurmountable.
Kepler had to discover a way of bringing order into this chaos. To start with , he saw that it was necessary first to try and find out about the motion of the Earth itself.
As Einstein noted, the motion of the planets in the solar system is not directly observable. One can only observe the relative positions of the Sun, the planets and the fixed stars, as viewed from the Earth. The observed changes in these relative positions are thus due to a combination of motions. Therefore, to determine, for example as Kepler sought to do, the motion of the planet Mars, it was first necessary to untangle which part of the observed changes in the relative positions of Mars, Earth, Sun and fixed stars are due to the motion of each.
Kepler had demonstrated in The New Astronomy, Ptolemy, Copernicus, and Brahe all found different mathematical means to untangle these motions. The problem for Kepler was that none of them were, or even claimed to be, true. Kepler, following Cusa, sought to understand the observed motions as a function of the true causes. But he could not directly observe these causes, so he had to surpass the limitations of sense-perception, and imagine the observed motions from a vantage point that was accessible only through reason.
But before determining the true causes, Kepler had to know the observed motions which also required him to surpass the limitations of sense-perceptions. In the case of the observed motions of Mars, Kepler had to first determine the relationship of Mars to the Earth and the Sun. This meant knowing the motion of the Earth, which he could not directly observe. Consequently, he had to imagine how the motion of Earth would appear were he to observe it from Mars, whose motion he didn’t know!
His approach is detailed in The New Astronomy, but its outline is as follows. From the Earth, one can observe the apparent motion of the Sun through the zodiac over the course of a year. Kepler understood this apparent motion of the Sun to be a reflection of the actual motion of the Earth. The cyclical nature of this motion indicated clearly, that the Earth’s motion was a closed orbit. In this way, he could imagine how an observer on the Sun would view the Earth.
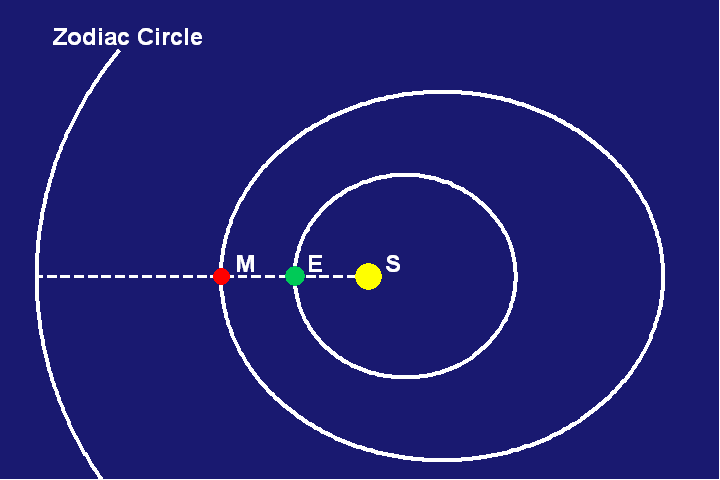
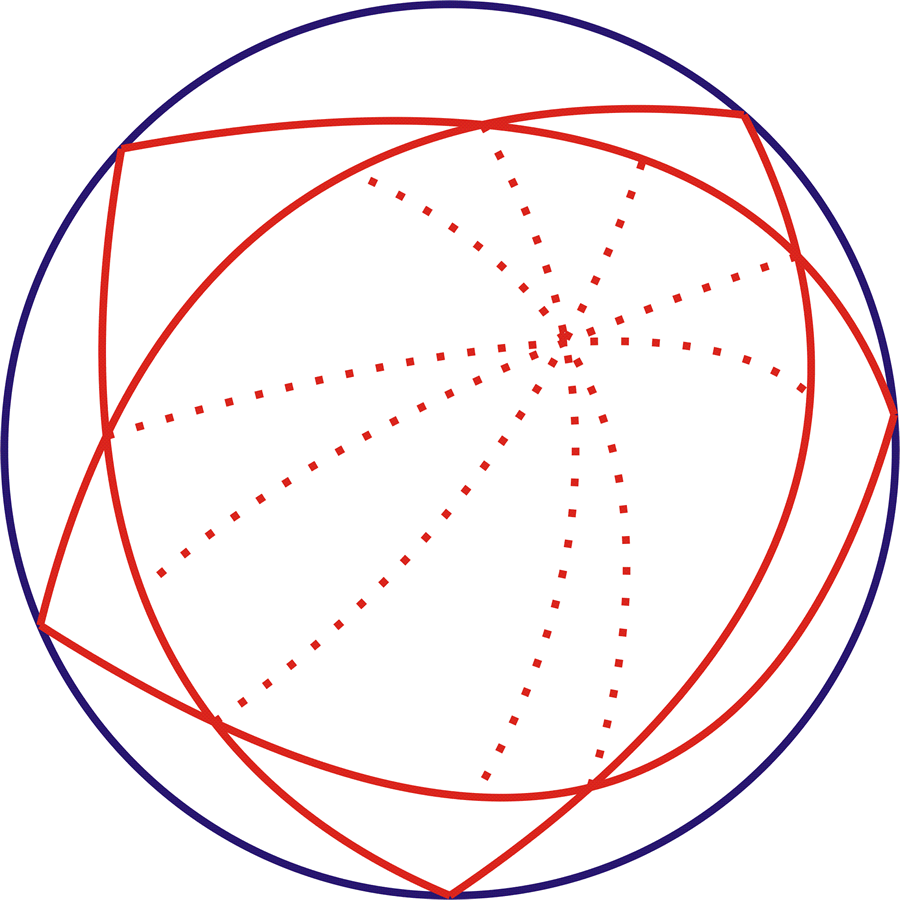
To view the Earth from Mars was more problematic, because, unlike the Sun, Mars was also moving. To solve the problem, Kepler began by noting the position in the zodiac of Mars and the Sun at the unique moment when the Sun, Earth and Mars are in a direct line with each other. (See Figure 1.)

This configuration is called opposition, which most recently occurred on November 7, 2005. At this moment an observer on the Earth will see Mars at a certain place in the zodiac, and an observer on Mars would see both the Earth and the Sun at a place in the zodiac directly opposite the position of Mars.
At some point following this observation (historical observation had determined that this period was 687 Earth days), Mars will return to the same position in its orbit as when it had previously been in opposition with the Earth and the Sun. But, the Earth will be in a different place in its orbit, and because of this, Mars will be observed in a different place in the zodiac! (See Figure 2.)
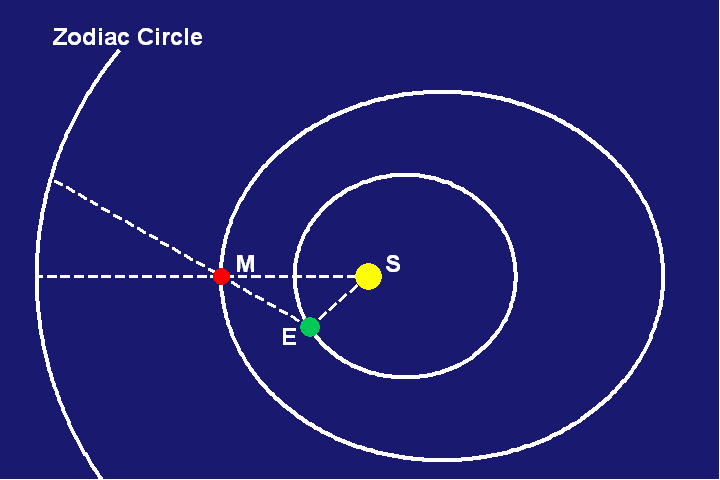
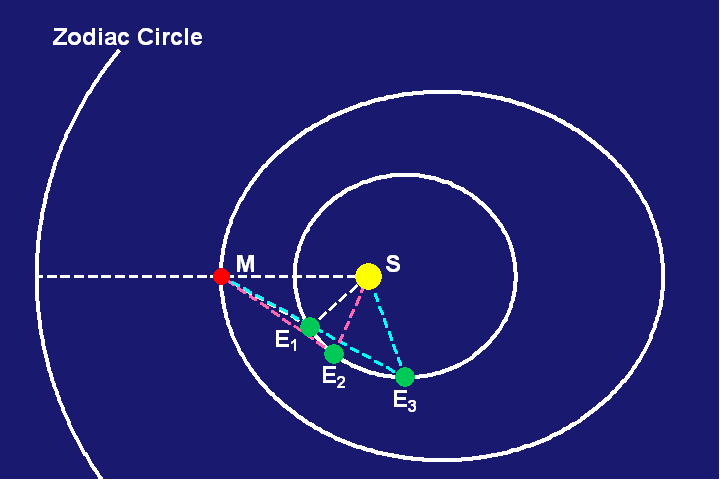
Nevertheless, an observer on Mars would now observe the Sun in the same place in the zodiac as it had been 687 Earth days earlier. But, he would see a change in the Earth’s position in the zodiac between the two periods. These observations form a triangle among the Earth, Sun and Mars, whose base is the direct line formed by the three objects at the first opposition, and whose legs are formed by the lines of sight from the Earth to Mars and the Earth to the Sun at this new position of the Earth. By comparing the observations from these three vantage points, Kepler could determine the angles of this triangle. By repeating this calculation, using Tycho Brahe’s extensive twenty year record of observations, Kepler was able to determine a precise orbit of the Earth. (See Figure 3.)
Having determined the orbit of the Earth, Kepler then turned to determining the orbit of Mars. The extensive record of Kepler’s discovery is detailed in The New Astronomy to which the reader is referred, but there is one point that is crucial to emphasize for what will follow.
After Kepler determined the size of the Earth’s orbit and its eccentric position relative to the Sun, he found that Mars’s orbit was also eccentric relative to the Sun. His first assumption for the orbits of both Mars and Earth was that both orbits were circular. For the Earth, this served as a successful approximation because the Earth’s eccentricity is quite small. However, for Mars, the eccentricity deviated from pure circularity by a significant amount. Kepler discovered this by testing the observed positions of Mars against the geometrical characteristics of a circle: specifically, that three distinct positions are sufficient to determine a unique circle. Under this assumption, any three observed positions of Mars would lie on the same circle. But, after testing 79 sets of three observations each and found that each set of three lay on a different circle. Kepler then realized that he was not dealing with a circular orbit and after much work, he showed that this orbit was an ellipse, with the Sun at one of the foci.
Untangling the Shadows
As noted above, in seeking to determine the orbit of Mars, Kepler was seeking to determine the nature of the Universe as a whole; a Universe that would produce a solar system with an Earth that had come to be dominated by life and inhabited by cognitive human beings who were discovering its principles.
Kepler realized that to investigate these deeper principles through astronomy, he had to also investigate the process by which he was investigating. Just as he had to determine the motions of the solar system from inside the solar system, to determine the underlying nature of the Universe, he had to form a self-conscious conception of the role of his own mind in the development of that Universe. This meant that he had to investigate: the connection between the physical parts of the Universe, the interaction of those physical parts with his senses, the interaction of those sense perceptions with his mind, and the interaction of his mind with the Universe as a whole.
He recognized that since all astronomical observations result from an interaction of light and the human eye, knowing the principles of light and vision would provide a link to the connection between the cognitive and physical domains. As he wrote in the introduction of his Optics:
What wonder, then, if that principle of all adornment in the world, which the divine Moses introduced immediately on the first day into barely created matter, as a sort of instrument of the Creator, for giving form and growth to everything–if, I say, this principle, the most excellent thing in the whole corporeal world, the matrix of the animate faculties, and the chain linking the corporeal and spiritual world, has passed over into the same laws by which the world was to be furnished.
In the Optics, Kepler elaborates that this coherence between the laws of physics and cognition is reflected by expression of the elliptical planetary orbits and the characteristics of light and vision as special cases of a single conception of a conical function.
It is important here to dispel the popular myth that is repeated in virtually every high school and university mathematics department today. Today’s mathematicians, being the artful dodgers they are, insist that the Greeks investigated the conic sections only for their mathematical purity, without any regard for their significance in the physical world. Thus, these sophists maintain that, when Kepler discovered the elliptical nature of planetary orbits, it was a complete surprise, and incidental to the purely mathematical concerns of the Greeks.
Nothing could be farther from the truth. The Greek investigation of the conic sections arose out of the Pythagorean investigations of the problem of doubling the cube. As Plato states in the Timaeus, this was an investigation of the characteristics of the physical universe, the way these physical characteristics are truthfully reflected in the human mind, and, the interaction of the human mind with the Universe as a whole. Thus, Kepler’s discovery that the planetary orbits expressed another form of the same conical function, was not only not accidental, it was not a surprise, except to today’s mathematicians.
Further, when Kepler discovered the planetary manifestation of conic sections, he also understood this to be of universal significance, indicating, as did Archytas’s construction for the doubling of the cube by torus, cylinder and cone, that the characteristic of action in the physical universe is not simply spherical, but is of a higher type–a type that Gauss and Riemann would later call hypergeometric.
That higher type of hypergeometry begins to emerge through an investigation of the general form of a single conical function, from which the elliptical orbits and the doubling of the cube are physical manifestations. In his Optics, Kepler investigated this conical function from the standpoint of light and vision.
From one perspective, the conic sections can be generated by the motion of a plane cutting a cone. (see Figure 4.)
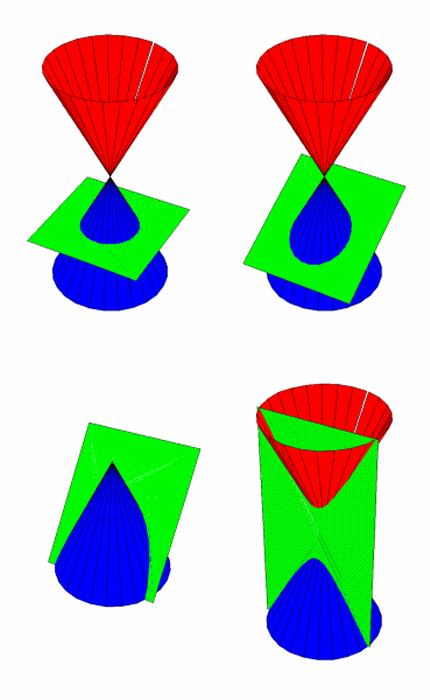
However, if viewed as a projection onto a surface, a mathematical discontinuity appears, in the transition from the region of elliptical action to the region of the hyperbolic. (See Figures 5a-b.)

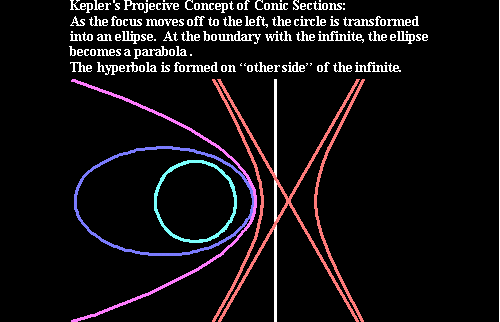
As Kepler describes it:
Speaking analogically rather than geometrically, there exists among these lines the following order, by reason of their properties: it passes from the straight line through an infinity of hyperbolas to the parabola, and thence through an infinity of ellipses to the circle. For the most obtuse of all hyperbolas is a straight line; the most acute, a parabola. Likewise, the most acute of all ellipses is a parabola; the most obtuse, a circle. Thus the parabola has on one side two things infinite in nature–the hyperbola and the straight line–and on the other side two things that are finite and return to themselves–the ellipse and the circle. It itself holds itself in the middle place, with a middle nature. For it is also infinite, but assumes a limitation from the other side, for the more it is extended, the more it becomes parallel to itself, and does not expand its arms (so to speak) like a hyperbola, but draws back from the embrace of the infinite, always seeking less although it always embraces more. With the hyperbola, the more is actually embraced between the arms, the more it also seeks. Therefore, the opposite limits are the circle and the straight line: the former is pure curvedness, the latter pure straightness. The hyperbola, parabola, and ellipse are placed in between, and participate in the straight and the curved, the parabola equally, the hyperbola in more of the straightness, and the ellipse in more of the curvedness.
Kepler further showed that the epistemological implications that the planetary orbits are elliptical, is not only expressed in relationship to light and vision. Most notably in his Harmonies of the World, he demonstrated the congruence between the relationships of the determining minimum and maximum speeds among the elliptical orbits, and the relationships of well-tempered polyphony that J.S. Bach subsequently developed through his compositions. Here again, a discontinuity appeared that had a physical significance. Specifically, the existence of the Lydian intervals formed between the orbits of both Mars and Jupiter and the yet to be discovered asteroid belt! This physical discontinuity as a point of change (a type of register shift), is also reflected in the difference in the physical nature of the planets that inhabit different sides of this discontinuity. This harmonic relationship, and the accompanying discontinuity are hereditary reflections of the harmonically organized plasma disk from which the solar system developed.
The subsequent discovery of the hyperbolic orbits of comets, and Gauss’s determination of the orbit of the asteroid Ceres, showed that Kepler’s understanding that the elliptical orbits are a special case of a more general conical function, was correct. This generalized understanding of Kepler’s astronomy was summarized by Gauss in his Theory of the Motions of the Heavenly Bodies Moving About the Sun in Conic Sections.
Gauss, and his student Riemann, went still further, specifying that Kepler’s general conical function was itself a special case of a more general, higher, hypergeometric, or hyper-conical function. These hypergeometric functions expressed, not the characteristics of the solar system per se, but the form of the universal characteristics that generated the characteristics of the solar system.
The Non-Infinite Universe
In locating the conical functions from the standpoint of a unified conception of the physical, biological, and cognitive domains of astronomy, Kepler was advancing the process, begun by Cusa, of returning science to the higher conceptions of the ante-Euclidean Greeks, and presaging the later achievements of Kaestner, Gauss and Riemann. This meant purging science of the pernicious effects of the slavish acceptance of Euclidean geometry.
A crucial point of attack for Cusa and Kepler was to demolish the false and arbitrary Aristotelean concept of the mathematical infinite enshrined in Euclid’s Elements. If space were as Euclid claimed–infinitely-extended in three rectilinear directions–only uniform circular or rectilinear motion would be possible. In such a fantasy world, the experimentally determined non-uniform elliptical orbits could only exist as arbitrary aberrations in a world that was assumed not to change.
As Abraham Kaestner later stated, the formal validity of Euclidean geometry rises or falls on the acceptance of the parallel postulate. Euclid was so aware of this vulnerability that he did not directly mention infinity in its statement, and he cited the parallel postulate only sparingly in the proofs of the theorems that follow. Nevertheless, as Kaestner and Gauss both underscored, without the assumption of the parallel postulate, there are no similar triangles, and without similar triangles, the entire edifice of Euclidean geometry crumbles. Gauss went further than Kaestner, emphasizing that the parallel postulate could only be true if one assumed that the curvature of physical space were zero– a fact which could only be determined by physical measurement, not by the mathematical formalism of Euclidean geometry.
From a subjective standpoint, the belief in a physical reality for Euclidean geometry requires the acceptance of Kant’s axiom that the human mind must be virtually hard-wired to think of the Universe in Euclidean terms. However, such ancient demonstrations as Archytas’s proof that doubling the “Euclidean” cube depends on a higher conical function, already demonstrates that Kant’s reverence for Euclidean geometry is false. Kepler’s projective construction of the conical sections, provides a further demonstration that such a Kantian view is completely illusory.
In Kepler’s construction, the infinite appears, not as an unreachable, indefinite magnitude, but as a point of change–a transition between the elliptical and hyperbolic domains of action joined by a single conical function. Thus, from Kepler’s standpoint, the infinite is in the middle, not at the end, of a non-infinite self-bounded manifold.
The experimental and epistemological arguments for such a concept of a non-infinite Universe were already presented by Plato in the Timaeus . Cusa and Kepler revived and extended these discussions in many locations. In his On Learned Ignorance, Cusa emphasized that the apparently infinite emerges in the “unfolded” form of a self-bounded, “enfolded” Universe. In the unfolded form, opposites, such as the minimum and maximum appear different, but in the enfolded form, such opposites coincide. In 1610, Kepler stated a physical argument for Cusa’s self-bounded conception: if the Universe were infinite, the night sky would not be dark but would be filled with light from an infinite number of stars. This paradox is today associated with Gauss’s close collaborator, William Olbers, who, nearly two hundred years later restated it as a direct argument against Kant.
In his habilitation dissertation, Riemann also stated the case for a non-infinite Universe:
When constructions in space are extended into the immeasurably great, unlimitedness must be distinguished from infiniteness; the one belongs to relations of extension, the other to those of measure. That space is an unlimited, triply extended manifold is an assumption applied in every conception of the external world; by it at every moment the domain of real perceptions is supplemented and the possible locations of an object that is sought for are constructed, and in these applications the assumption is continually being verified. The unlimitedness of space has therefore a greater certainty, empirically, than any experience of the external. From this, however, follows in no wise its infiniteness, but on the contrary space would necessarily be finite, if one assumes that bodies are independent of situation and so ascribes to space a constant measure of curvature, provided this measure of curvature had any positive value however small.
As Cusa emphasized, this anti-Euclidean notion of a self-bounded Universe, conforms to the nature of both the physical world and Man. Like the physical world, man’s life is finite but unbounded. It begins at birth and ends at death. From this standpoint of mortality, the world before birth and the world after death, appear to be infinitely far way. But that finite life, through the transmission of creative discoveries through culture, affects, and is affected by, what precedes and follows it. The apparently infinite domains, beyond the temporal limits, are not outside one’s mortal life, but at the center of it. Thus, to believe in a Euclidean geometry is to reject the immortality of the human soul.
Cusa’s and Kepler’s annulment of Euclidean geometry set the stage for the development of a new, physically determined concept of a non-infinite geometry. The first steps taken in that direction are due to the work of Girard Desargues (1593-1662) who junked Euclidean geometry in favor of Kepler’s notion of projective relationships, thus, banning the Aristotelean concept of the infinite completely from science.
A simple experiment can be performed to illustrate Desargues’ method. Draw a large rectangle on a whiteboard. The opposite sides of the rectangle would appear, from the assumptions of Euclidean geometry, to be parallel, and thus never meet, even if infinitely extended. Now take a transparent pane of plexiglass and tilt it at an angle to the plane of the whiteboard. With one eye closed, trace the outline of the rectangle onto the plexiglass. This action produces a conical projection of the whiteboard onto the plane of the plexiglass, with the eye as the apex of the cone. Under this projection, the images of the opposite sides of the rectangle, that appeared to be parallel on the whiteboard, now intersect on the plexiglass. Thus, with a turn of the head, the infinite is brought into the finite!
In this way, Desargues began to generalize Kepler’s elaboration of Cusa’s idea of a non-infinite Universe producing many important discoveries that are crucial for the later development of science, one of which is particularly important for our argument here.
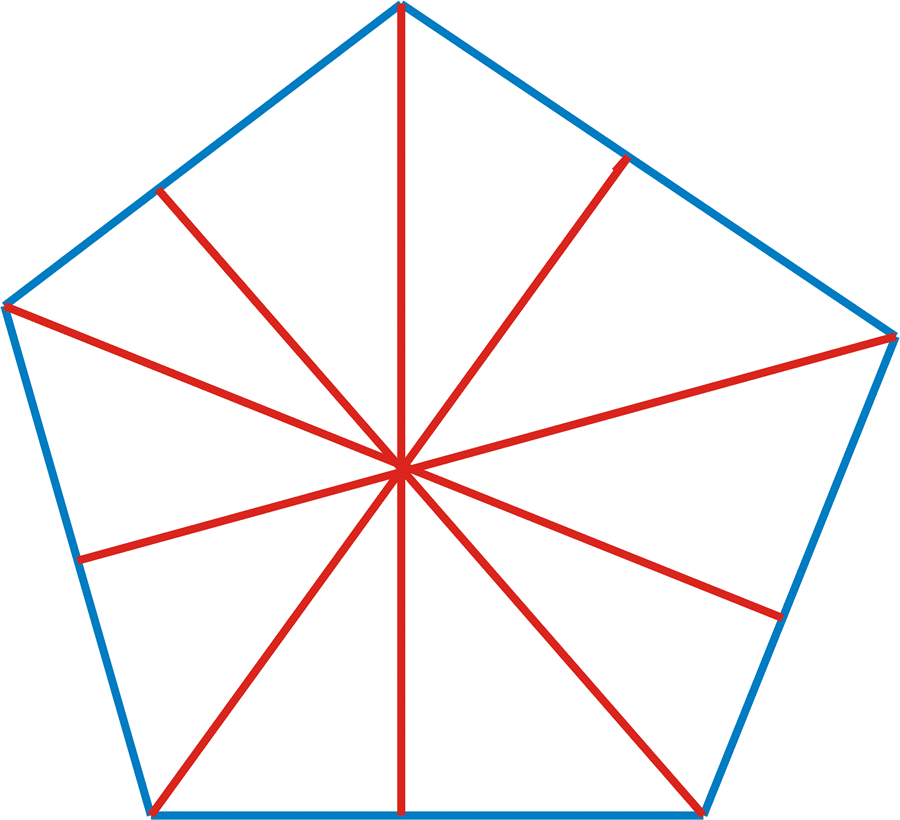
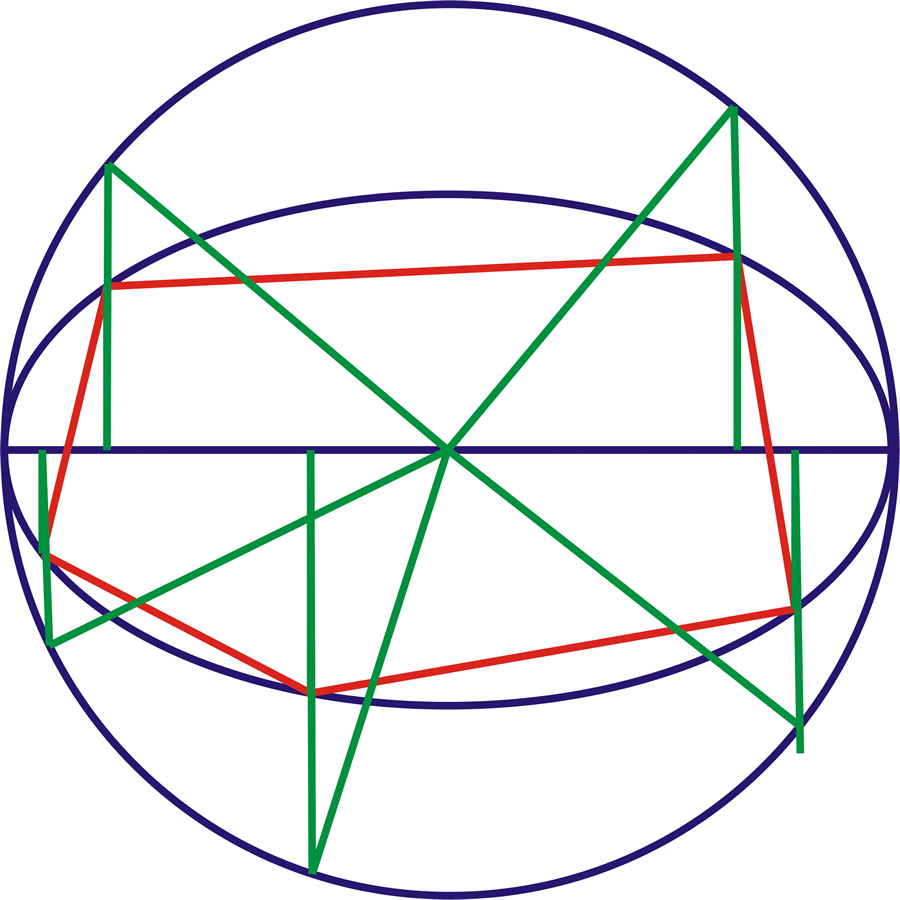
Desargues showed that, though under projection lengths, proportions of lengths and angles are, in general, changed, there is one characteristic that remains invariant. Later called the cross-ratio, this characteristic is the ratio of two ratios formed among four arbitrary points. (See Figure 6.)
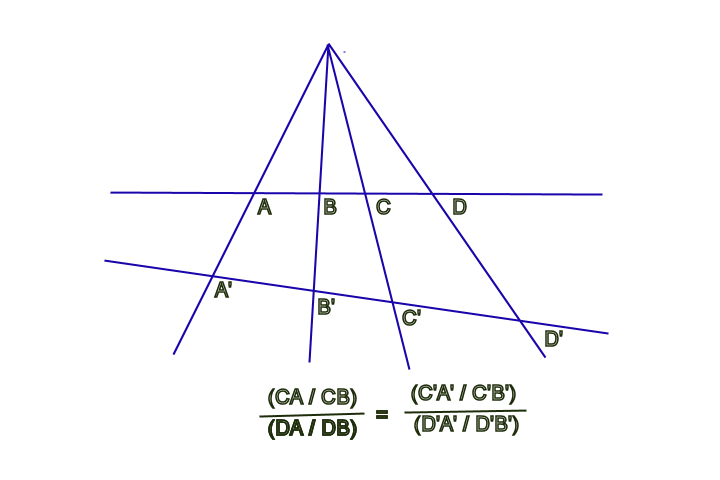
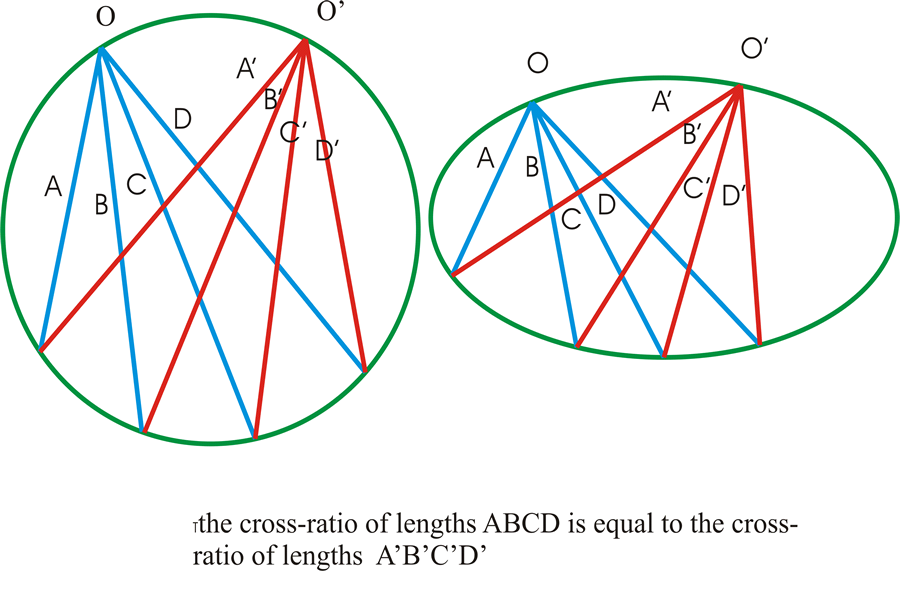
Since the conic sections are in a projective relationship to each other, the invariance of the cross-ratio is a characteristic of the conical function. (See Figure 7.)
A further illustration of this same principle can be taken from another discovery of Desargues–the complete quadrilateral. Desargues proved that the intersections of the extended sides and diagonals of an arbitrary quadrilateral form a projective configuration in which the cross ratios are preserved. (See Figure 8.)
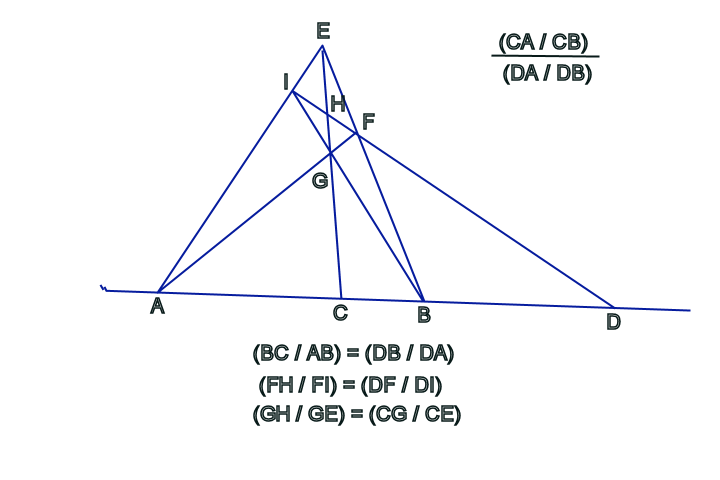
This type of cross ratio is a special case, called harmonic, because B divides segment AC in the same proportion that C divides AD. If one now looks at the complete quadrilateral dynamically, and imagines, in the tradition of Kepler, that point D moves off towards the infinite in one direction, the position of points A, B and C must also move in order to maintain the harmonic relationship among all four points. This motion will also change the angles of the quadrilateral. (See Figure 9.)
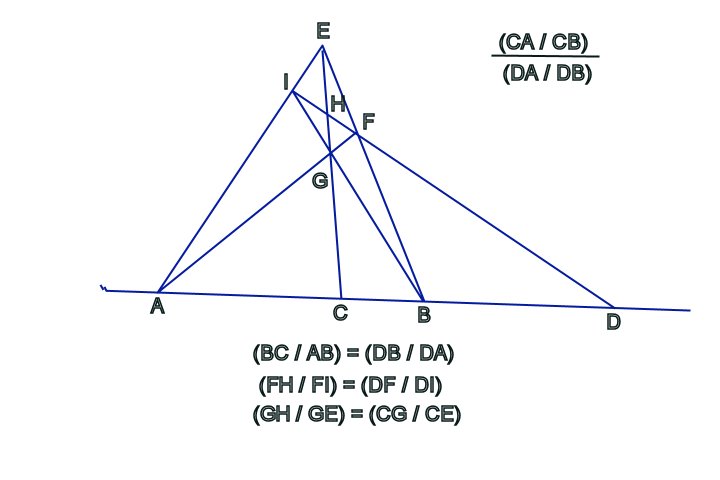
When the sides of the quadrilateral become parallel, point D reaches the infinite, or, inversely, when D reaches the infinite, the sides of the quadrilateral become parallel. At this point, the harmonic cross ratio with points A, B and C is still maintained. (See Figure 10.)
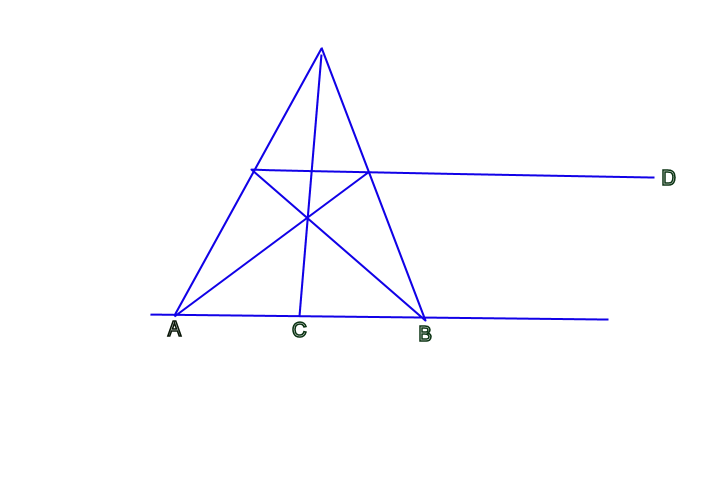
If we now tilt the sides of the quadrilateral a little more, point D appears to return from the infinite on the other side of point A, all the while maintaining the harmonic proportions with points A, B, and C. (See Figure 11.)
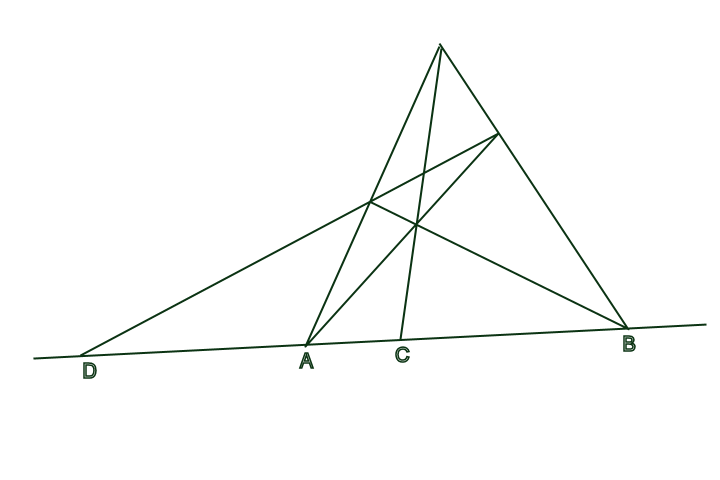
From the standpoint of Euclidean geometry, the harmonic characteristic of the complete quadrilateral seems mystical, because in Euclidean geometry, the infinite can have no effect on the finite. But as Desargues’ construction demonstrates, the “infinite” in the complete quadrilateral, is, as in Kepler’s projective conics, a single point of change, which maintains an harmonic relationship to the finite parts, just as any “finite” point does. This type of paradox confronts the dilemma of Euclidean sophists: either, maintain Euclidean geometry and insist that the harmonic characteristics of the complete quadrilateral are magic, or, recognize, as Kepler did, that the experimental evidence that physical principles express such harmonic relationships, and admit that Euclidean geometry is a fraud.
The complete quadrilateral also illustrates an early expression of what would later be called by Riemann, “Dirichlet’s Principle”. There is a single connected relationship among the position of points A, B, C and D, and the angles and lengths of the sides and diagonals of the quadrilateral. This relationship is an effect of the harmonic principle reflected by the invariance of the cross-ratio. It is this harmonic principle that is primary. The positions of the visible objects are a function of that harmonic principle.
The harmonic relationship exists, even if one of the points appears to be infinitely far away because the point at infinity is not outside the process, but within it. What appears to be infinite is merely a point of change, within an otherwise non-infinite self-bounded manifold.
The complete quadrilateral, and Kepler’s conics cannot exist in a Euclidean infinitely-extended space, but only in a Cusan-Keplerian non-infinite self-bounded manifold. In such a manifold, change is an essential characteristic and what appears to be mathematically infinite is understood as an expression of that change.
The Road to the Hyper-conical
After Desargues’ the nature and physical expression of Kepler’s conical function was elaborated further by Blaise Pascal and Leibniz. In his development of the infinitesimal calculus, Leibniz showed that the conical function had three distinct but related forms: the exponential, circular and hyperbolic. Through his collaboration with Bernoulli, Leibniz demonstrated that the catenary is a physical expression of the three forms of conical functions. This showed, once again, that the physical characteristics of the Universe conformed to the Cusan-Keplerian concept of a non-infinite self-bounded manifold. However, already embedded in Kepler’s astronomy was experimental evidence that these conical functions must be superceded by a higher type of hyper-conical function. This manifested itself in the so-called “Kepler Problem”, whose investigation led Gauss to first discover what he called the elliptical transcendentals.
The “Kepler Problem” arose from the effort to determine the motion of a planet in an elliptical orbit. Kepler had already shown that it was impossible to completely describe the principle on which this motion was based with respect to the functions of circular action. The subsequent work of Leibniz not only confirmed this, but also indicated that the other functions associated with conical action–the hyperbolic and exponential–were also inadequate to describe the motion of a planet in an elliptical orbit. As early as 1797 Gauss recognized that this was because elliptical motion is governed by the elliptical transcendentals, which are a distinct and higher form than the simple circular, exponential and hyperbolic functions.
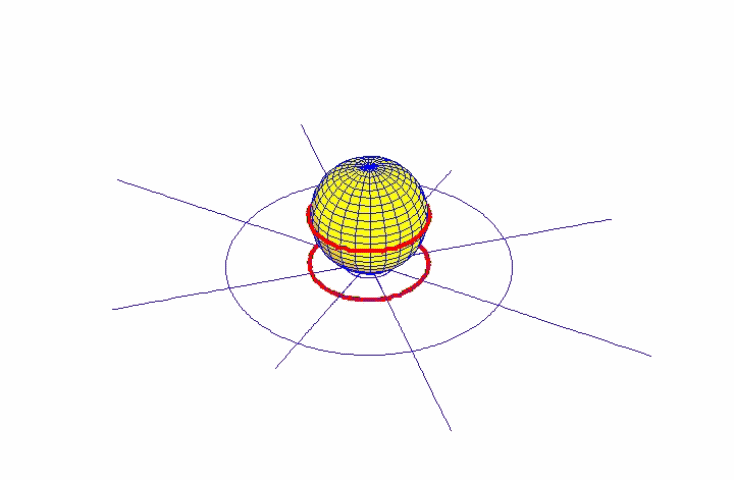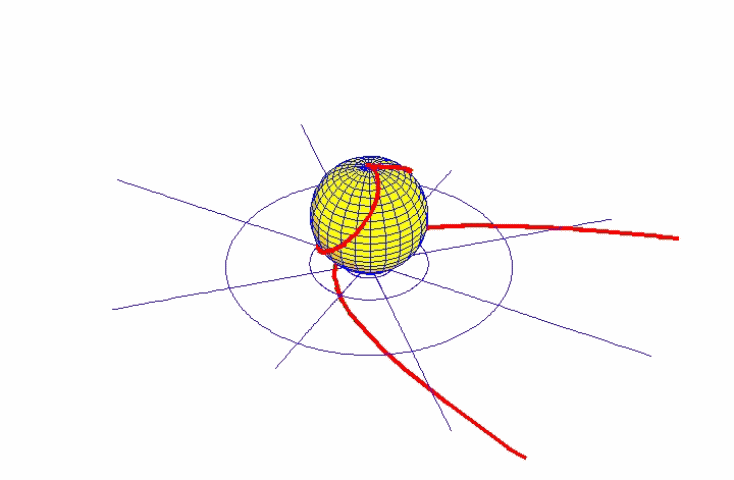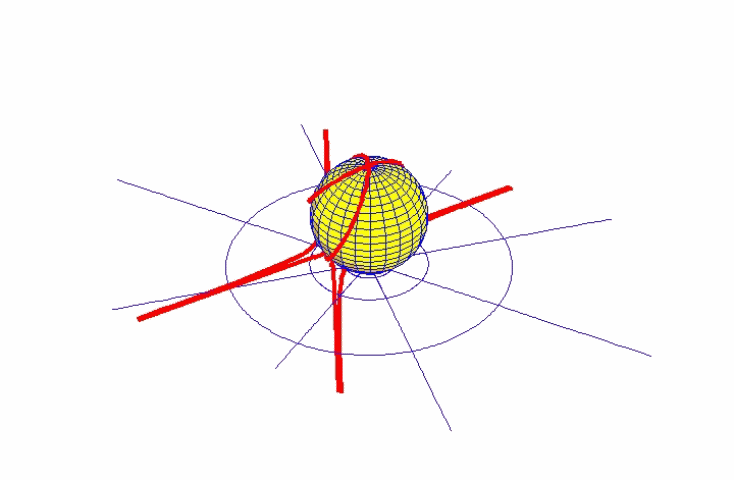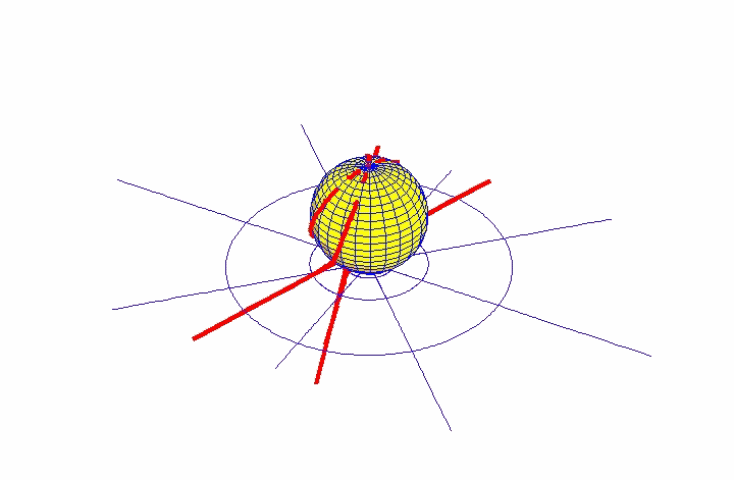
Subsequent to these early discoveries, Gauss continued to explore the relationship between these two transcendental domains. One of his most intriguing insights is expressed by his investigations of the pentagramma mirificum. The pentagramma mirificum was originally discovered by Kepler’s contemporary John Napier in connection with his investigations of spherical trigonometry. Napier had recognized that the self bounded nature of the sphere is reflected in the connected relationship between the sides and angles of a spherical triangle. In such a spherical triangle, the lengths of the sides are a function of the angles and vice versa. In the special case of a spherical right triangle, this relationship is expressed by the pentagramma mirificum.
Unlike a Euclidean triangle, in which the sides are measured as lengths, in a spherical triangle, both the sides and the angles are measured as angles. (See Figure 12.)
Napier showed that in a right spherical triangle, the three sides and two other angles are connected to each other by a relationship between their sines and cosines. (See Figure13.).
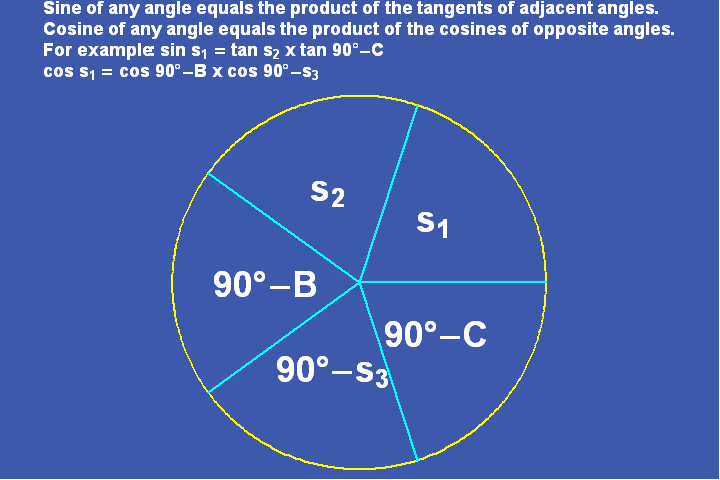
The relationship among these five components can be ordered so that they form a self-polar spherical pentagon, which Napier called, the pentagramma mirificum. (See Figure 14.).
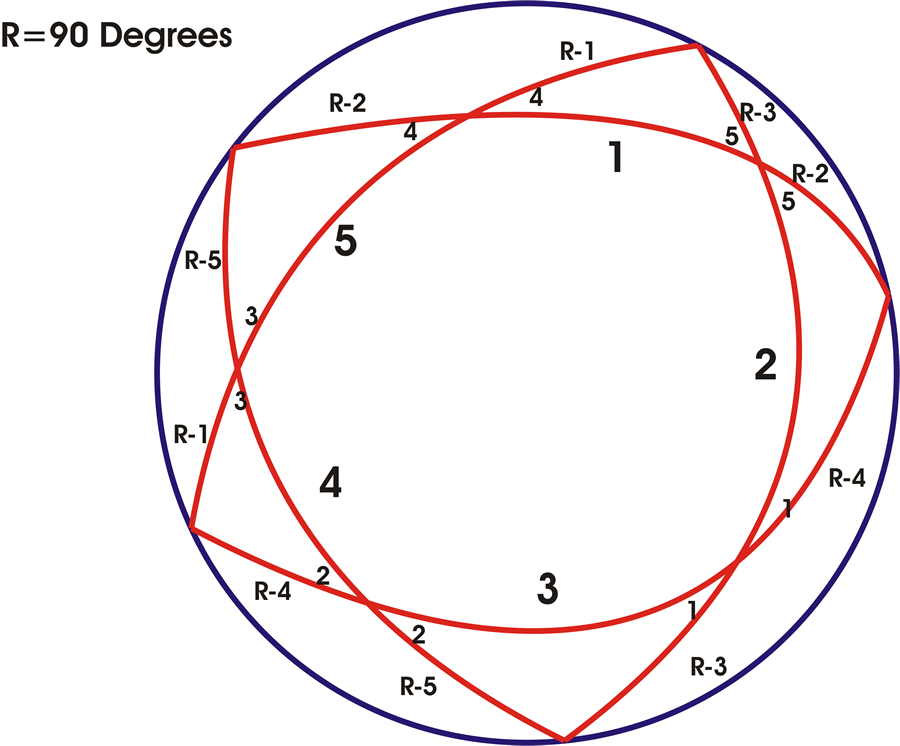
Gauss was intrigued by the relationship of Napier’s spherical pentagram to his elliptical transcendentals. He realized that Napier’s pentagramma mirificum established that a spherical surface had an intrinsic five-fold periodicity. He saw this five-fold periodicity in light of a well known discovery of Apollonius that five points are required to uniquely determine a conic section. This distinguishes the general conic section from a circle, which requires only three points, and a line, that requires only two. Gauss recognized that the five-fold periodicity of the sphere and the five point determination of conics, reflected the distinction between the higher form of elliptical transcendentals and the lower form of transcendental associated with circular, hyperbolic and exponential functions.
These simple transcendentals, associated with Kepler’s conical function, arise in connection with physical action characterized by a single principle of change, such as the incommensurability between the arc and the sine in uniform circular motion. However, the elliptical transcendentals, as Gauss showed, are characterized by two principles of change, exemplified in an ellipse by the double incommensurability between the sine and the arc and the sine and the angle. A similar elliptical double incommensurability appears in a circular pendulum between the angle and the sine and the angle and the time.
The connection between the spherical pentagram and the elliptical functions is illustrated by Gauss’s demonstration that, when the spherical self-polar pentagon is projected onto a plane that is tangent to the sphere, by a cone whose apex is at the center of the sphere, a rectilinear plane pentagon is produced. (See Figure 15. )
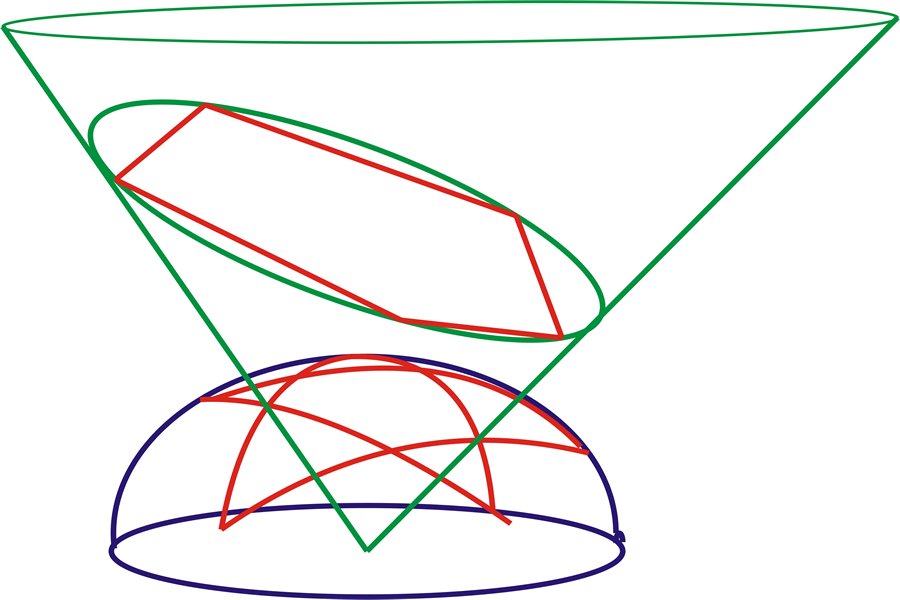
The five vertices of this plane pentagon define a unique ellipse. The altitude lines of this plane pentagon all intersect at one point, which is the image of the point of tangency of the plane to sphere. (See Figure 16.)
Gauss showed that this characteristic is a reflection of the fact that the vertices and opposite sides of the plane pentagon were images of poles and equators of the spherical self-polar pentagon. (See Figure 17.).
This reflected a type of “Dirichlet’s Principle” in that on the sphere, the altitude lines of the spherical pentagram can intersect at any point inside the spherical pentagon. However, on the plane pentagon there is only one set of altitude lines. Thus, the spherical self-polar pentagon reflects an entire manifold of plane pentagons, each of which reflects elliptical action. The relationship among these plane pentagons can only be expressed by an elliptical transcendental. Thus, the spherical pentagramma mirificum is an unfolded form of an elliptical function.
In his work on the pentagramma mirificum, Gauss then investigated this plane pentagon inscribed in an ellipse, in light of Kepler’s determination of the position of a planet in an elliptical orbit. (See Figure 18.).
He showed that this relationship, between the spherical pentagon and its projection, was expressed by his new elliptical transcendentals. This fact indicated that the characteristics of spherical action were implicitly elliptical and could not be completely characterized by circular functions, as naive sense-perception might indicate. Inversely, the fact that the experimental evidence demonstrated that the planetary motion is elliptical, not circular as Aristotle dogmatically insisted, demanded the rejection of naive notions of the sphere in favor of the higher forms of cognition indicated by Gauss’s and Riemann’s hypergeometric functions.
The Riemannian Self-Developing Domain
Just as Kepler’s method, provoked by the experimentally determined elliptical orbits, produced the concept of a non-infinite self-bounded conical function, that same method, provoked by the “Kepler Problem”, compelled Gauss to supercede Kepler’s result, (as Kepler himself demanded) producing the concept of the higher elliptical transcendental. However, such elliptical transcendentals are inadequate to express the higher forms of physical action which Riemann characterized as “multiply-connected continuous manifolds”. An adequate method to understand these types of physical action was not achieved until Riemann unified and advanced Gauss’s work on the hypergeometric functions. Further, just as Kepler’s elliptical orbits, and Gauss’s investigation of them, produced concepts of universal significance, Riemann’s investigation into physical processes governed by hypergeometric functions, produced a greater understanding of the Universe as a whole.
That understanding was elaborated in his Theory of Abelian Functions and his lectures on Gauss’s hypergeometric function. In those works, Riemann develops the power of Riemann surfaces to represent the concepts associated with multiply-connected hypergeometric action. Since the construction of Riemann’s surfaces has been treated in detail in previous installments of this series, we only summarize those constructions here.
Riemann recognized that the non-infinite, self-bounded manifold indicated by, Kepler’s conical function, or Desargues projective geometry conforms to a stereographic mapping of a plane onto a spherical surface. This “Riemann sphere” is a non-infinite, self-bounded surface, in which the north pole of that surface is the point of change, which is apparently infinite in the planar form. When Kepler’s conical function is projected onto the Riemann sphere, the apparently discontinuous conical function of Kepler beccomes a continuous function. (See Figure 19.).
The discontinuity between the elliptical and hyperbolic action remains, but on the Riemann sphere it is clearly represented, not as a Euclidean-type mathematical infinite, but as a singular point of change. A similar construction can also be imagined for Desargues’ complete quadrilateral.
Riemann showed that the simply periodic, circular, hyperbolic, and exponential transcendentals conform to the form of a non-infinite, self-bounded manifold expressed by a Riemann sphere. (See Figures 20.).
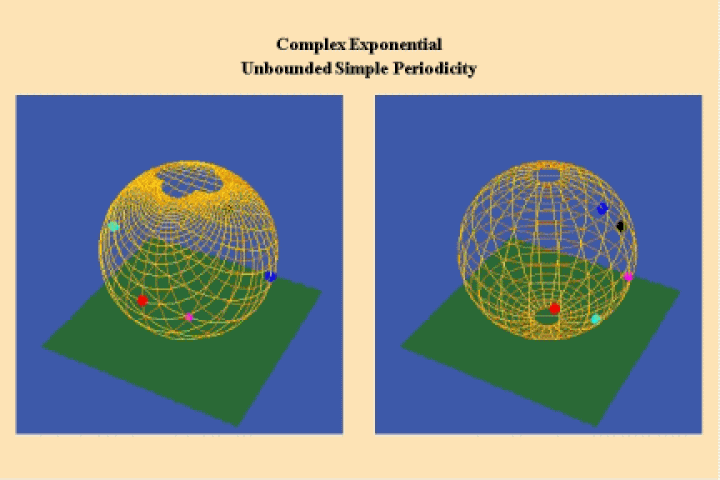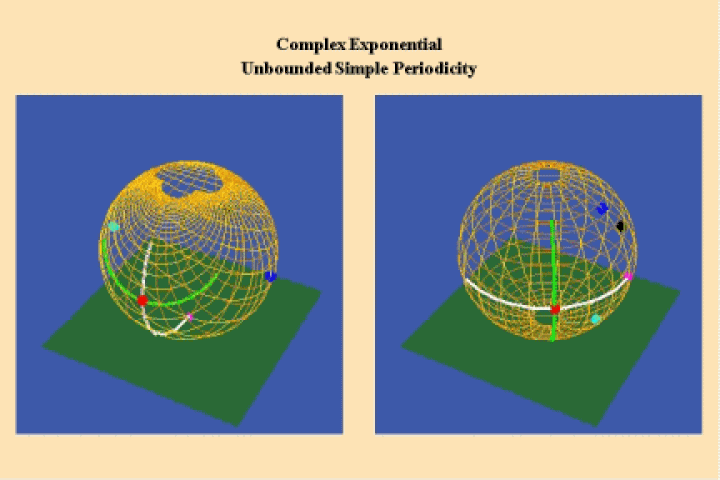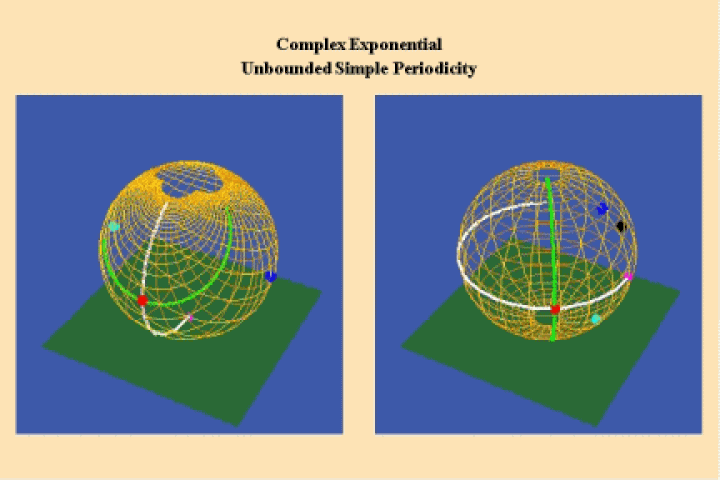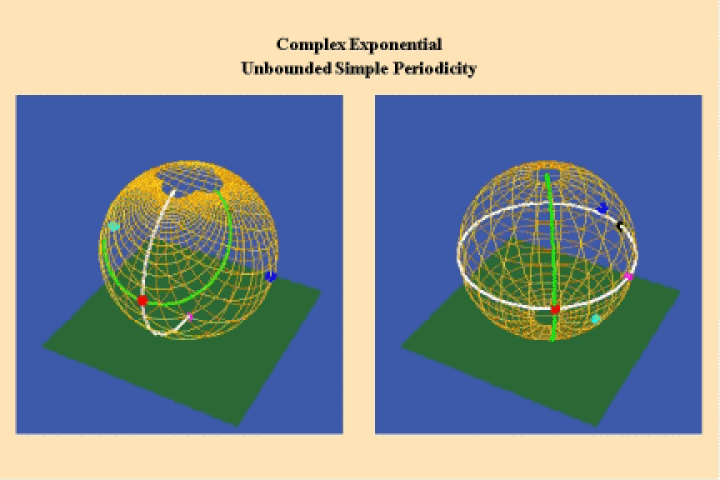
However, Gauss, Jacobi, Abel, and Riemann all showed that the doubly periodic elliptical transcendentals, produce four points at infinity. ( See Figure 21.).
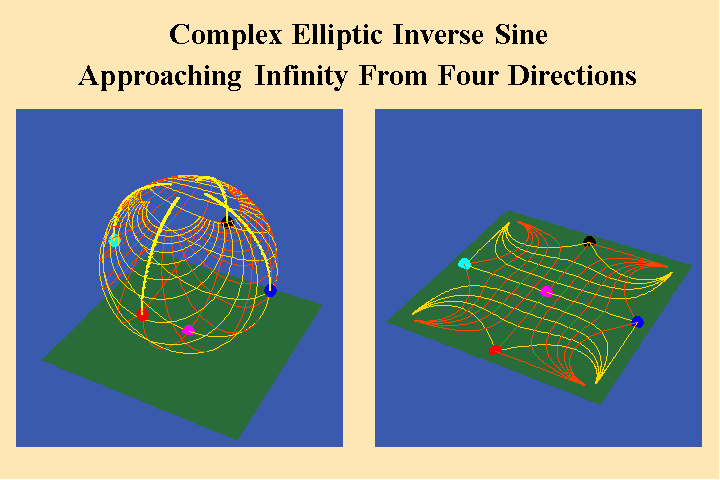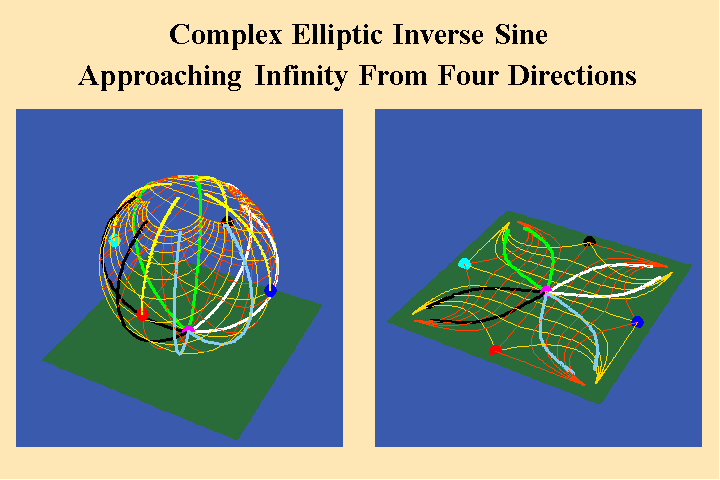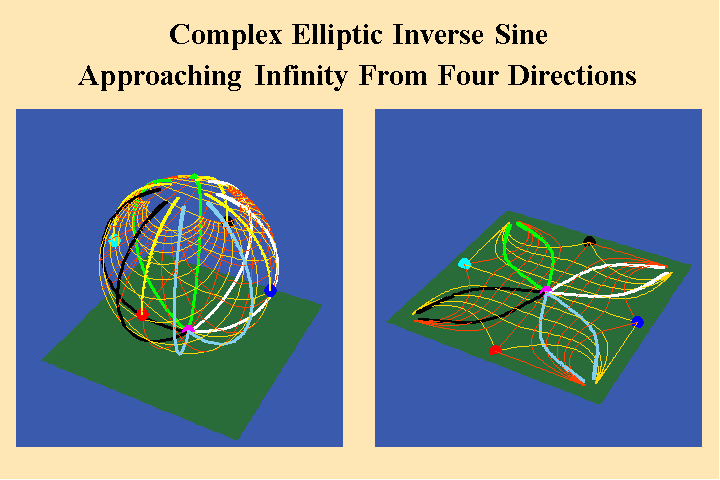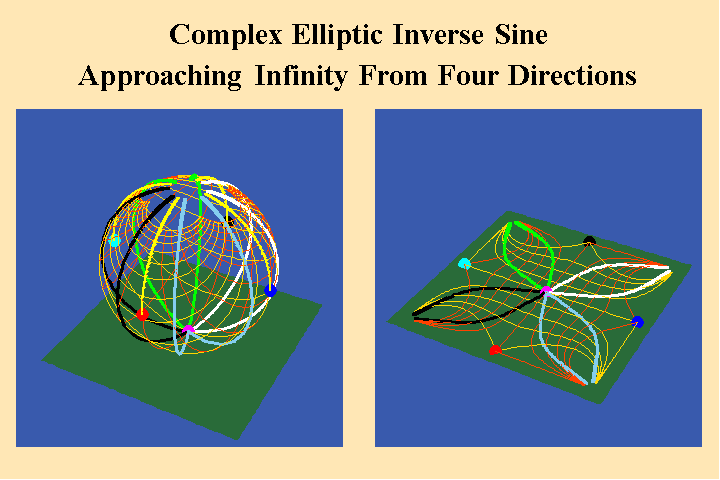
Riemann emphasized that a non-infinite, self-bounded manifold of four discontinuities cannot be represented in a spherical form. Rather, its geometrical characteristics conform to the shape of a torus. (See Figure 22.).

In continuing this investigation into the hyper-elliptical and Abelian functions, Riemann showed that each successive gradation of transcendental function, contained an increasing number of discontinuities. Consequently, each increase in the number of discontinuities is associated with a change in the characteristic (genus) of the associated non-infinite, self-bounded manifold. (See Figure 23.)

The geometrical representation of the change between manifolds of different genera is consistent with the topological difference between a sphere and a torus. That topological difference is expressed by the ability of the manifold to admit a greater number of distinct pathways of action. Thus, each successive species of non-infinite, self-bounded manifold, is capable of expressing physical action of successively greater complexity.
But just as Kepler’s treatment of conic sections from a projective standpoint revealed the underlying epistemological significance of elliptical motion, viewing this succession of self-bounded Riemannian manifolds in a projective form also unveils their true beauty.
Take as a starting point the simplest case: the self-bounded spherical manifold. The projection of this manifold is expressed by the projective relationship of Kepler and Desargues. Now, take the next case: the self-bounded torus associated with elliptical transcendentals. Its projective form is a parallelogram with four apparently infinite magnitudes. (See Figure 24.).
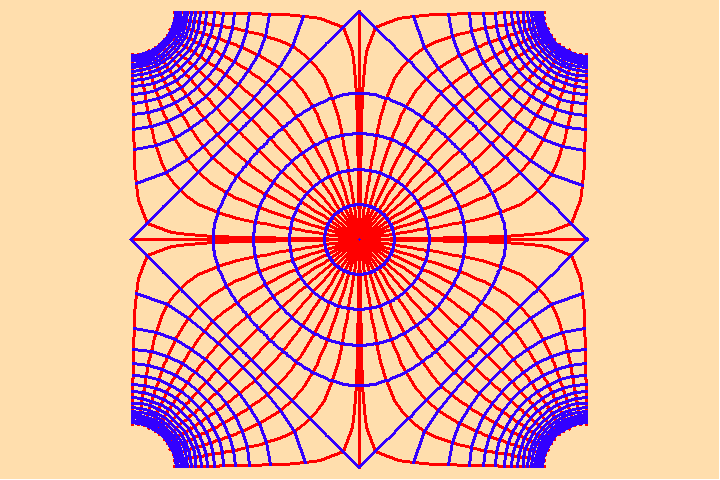
Consider this species of manifold, as Riemann did, as a manifold of physical potential. In this respect, the relationships between the orthogonal pathways of minimal and maximal change in potential, are determined, by the four apparently infinite magnitudes. Just as the “point at infinity” determines, for example, the harmonic characteristics of the complete quadrilateral, the four “points at infinity” of an elliptical transcendental determines the harmonic characteristics of this manifold. This is expressed, for example, by the transformation of the characteristic of the potential from a circular boundary near the center of the manifold, into a square boundary towards the edge.
However, we must consider the apparently infinite magnitudes in the elliptical transcendentals, not as “infinities” but as discontinuities within an otherwise self-bounded continuous process. In other words, just as Kepler’s conical function transformed the apparently infinite boundary between the elliptical and hyperbolic into a discontinuity within an otherwise continuous, self-bounded manifold, a similar means to “continue across the infinite” must be found for the elliptical transcendentals.
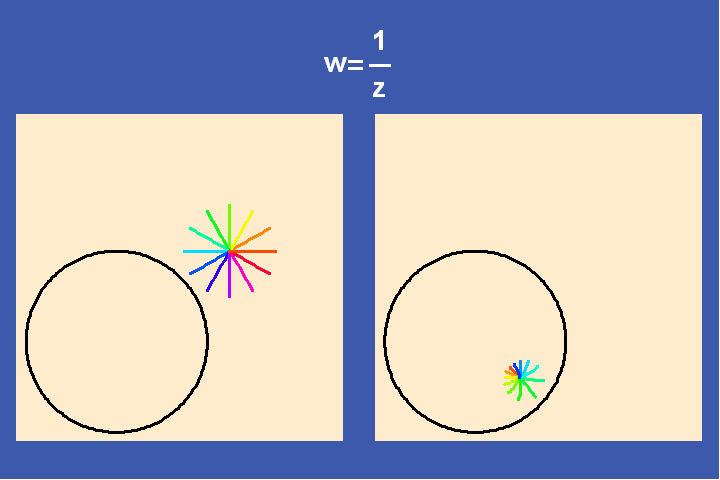
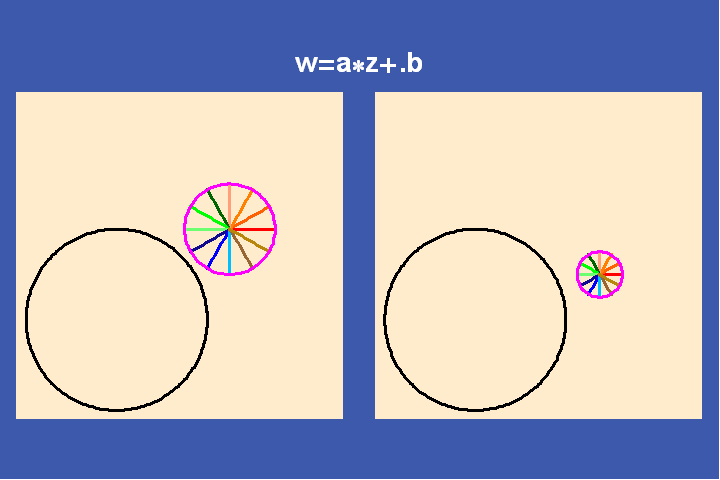
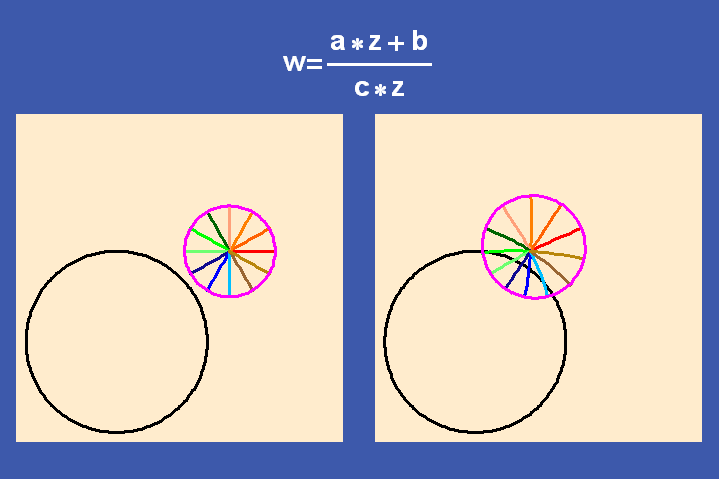
To do this, Riemann utilized a discovery of another student of Gauss, Ferdinand Moebius who elaborating Gauss’s treatment of complex functions. Moebius investigated the characteristics of what appeared to be the simplest type of complex functions: simple linear transformations, of the form (a*z+b)/(c*z+d), where z is a variable and a, b, c, d are arbitrary complex numbers. These Moebius transformations play a similar role with respect to the higher transcendental functions that the exponential functions play with respect to Leibniz’s catenary and the simple transcendentals.
Examples of simple transformations are translation, inversion, rotation, and combinations of all three. (See Figures 25a-f).
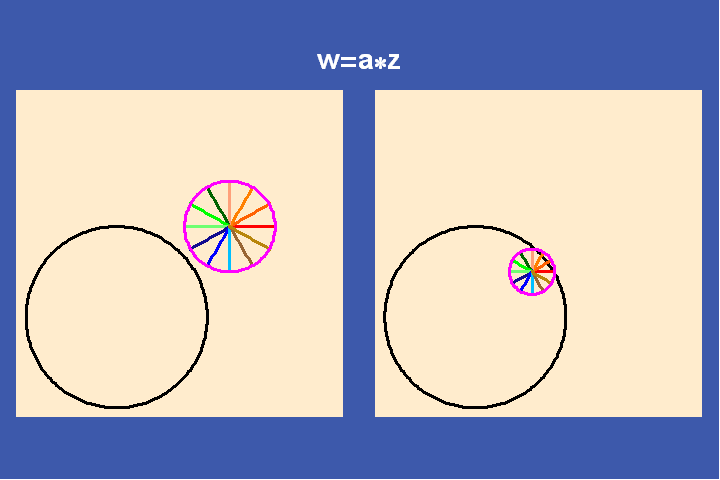
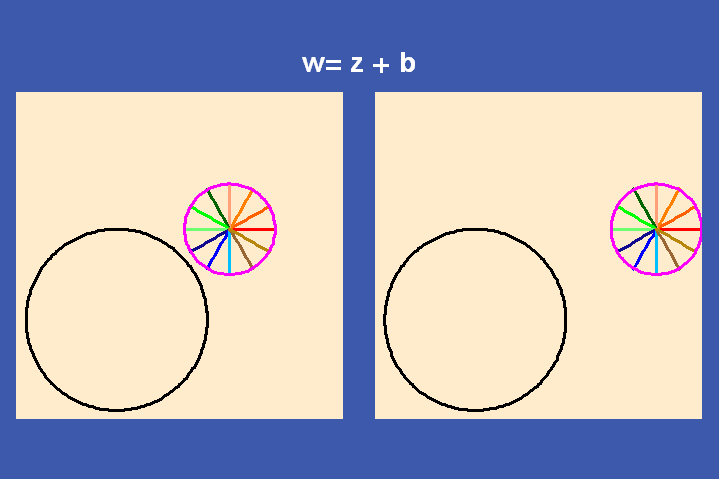
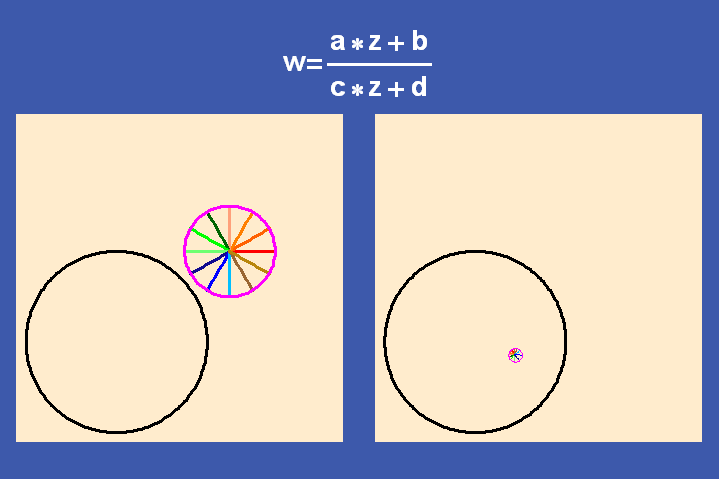
What Moebius discovered was that these simple types of complex transformations are actually generalizations of Kepler’s and Desargues’ projective geometry. Under these Moebius transformations, the cross-ratio among any four complex numbers is invariant. When the cross-ratio is a non-complex number, the four points lie either on a circle or a line. In keeping with Cusa, a line must be considered a circle whose center is the “point at infinity”.
A unique Moebius transformation can always be found that maps any three points to zero, one and infinity. Thus, it is most simple geometrically to define the cross-ratio, with respect to Moebius transformations, when three of the points forming the cross-ratio are zero, one and infinity. On a Riemann sphere, this means the points are at the south pole, the north pole and the equator. (See Figure 26.)
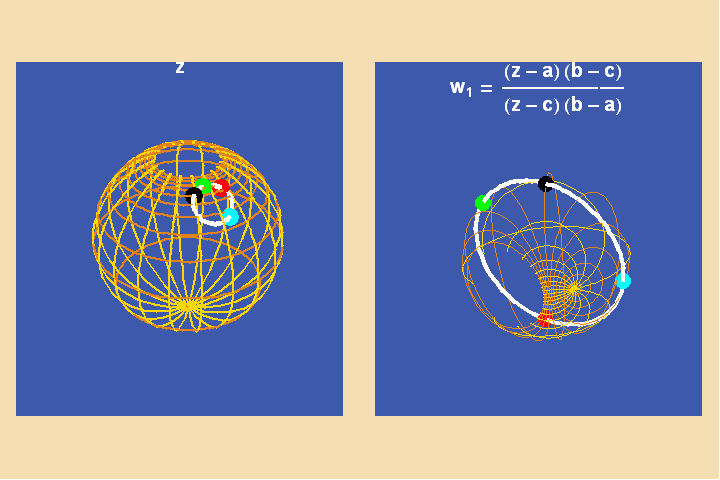
However, in the case of the elliptical transcendentals, there are four points that map to infinity and four points that map to one. Nevertheless, a simple set of Moebius transformations will continue this projection across the infinite. (See Figure 27.).
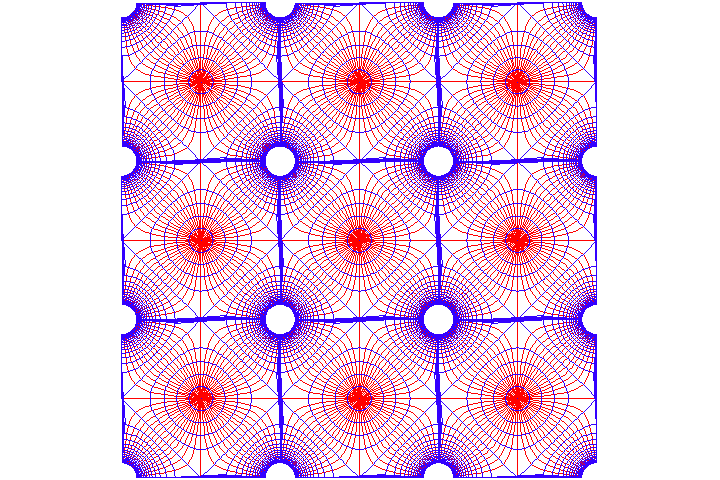
This gives us a projected image of the self-bounded torus, with a greater density of discontinuities than in is possible in a spherical manifold. (See Figure 28a,b.).


For the hyper-elliptical case, the projected image of the Riemann surface is a type of octagon with eight “points at infinity”, and eight points that map to unity. As in the case of the elliptical function, these eight points at infinity determine the harmonic characteristics of the manifold, but unlike the elliptical case, eight points at infinity are associated with a change to negative curvature. A different species of Moebius transformation continues this projection across the infinite. Thus, the hyper-elliptic function can only exist in a negatively curved, non-infinite, self-bounded manifold. (See Figure 29a,b.).


Such a manifold cannot be represented completely in visible space. Therefore, we can only “observe” such a manifold as a projection onto the cave wall of sense-perception.
However, it is important to underscore the significance of the change in characteristic curvature between the elliptical and hyper-elliptical. The spherical manifolds are characterized by positive curvature. The torus combines both positive and negative curvature for a net curvature of zero. The self-bounded manifolds of the hyper-elliptical and beyond are characterized by negative curvature.
From this standpoint, the discontinuity that appears in Kepler’s conical function between the elliptical and hyperbolic domains takes on a new light. It conforms to the change in characteristic between the generally positively curved manifolds of the simple and elliptical transcendentals to the negatively curved manifolds of the hyper-elliptic (hyperbolic) forms.
Riemann recognized the significance of this change and suggested that only a notion of space that encompasses all three types of curvature could adequately represent universal principles. In his habilitation dissertation he proposed an image for such a manifold as an intersecting sphere, cylinder and the negatively curved inner portion of a torus. (See Figure 30.)

One circle lies on all three surfaces, and forms the image of visible space.
Once again, the Euclidean plane of zero curvature does not exist, except in the minds of Aristoteleans and fools. It is merely a limited view of a manifold that is both positively and negatively curved. Such a manifold, represented by the torus of Riemann’s surfaces, or , metaphorically by, the cylinder in the above construction, is simply a transition between the predominately positively curved domain of visible space and the predominately negatively domain of the very large and very small.
Thus, the Universe cannot be characterized by a single type of curvature. Rather, it must be thought of as a dynamic process in which all three types of curvatures are interacting.
In this way, we can form from Riemann’s treatment of Abelian and hypergeometric functions, a concept, not of a single non-infinite, self-bounded manifold, but of a nested succession of such manifolds, a type of manifold of manifolds. Such a manifold of manifolds, which in Riemann’s representation, begins with the simple self-bounded sphere, continues to the torus, and then into the hyper-elliptical and higher functions, forms a concept of the form of a non-infinite, self-developing, self-bounded Universe.
A Final Look at Kepler, Riemann and Einstein
Einstein concluded his 1930 commemoration of Kepler saying:
It seems that the human mind has first to construct forms independently before we can find them in things. Kepler’s marvelous achievement is a particularly fine example of the truth that knowledge cannot spring from experience alone but only from the comparison of the inventions of the intellect with observed fact.
These closing statements reflect Einstein’s rejection of positivism, and echo, albeit in a weakened form, the influence of Kepler and Riemann on his thinking. Yet, they also point out his failing. Progress in science depends on developing a strengthened tie to Kepler and Riemann. The human mind does not “first construct forms independently before we can find them in things”, because it is never independent of the Universe in which it exists. The interaction of the intellect with observed fact, is not the interaction of two separate domains. It is an interaction which changes the self-developing, multiply-connected domains of physics, life and thought.
Kepler’s marvelous achievement is a fine example of this type of thinking. What is needed now, is more than simple admiration for Kepler. What is needed is an army of new Kepler’s, who, equipped with Riemann’s conceptions and LaRouche’s discoveries, will do as Kepler did during that brief interval of time that ended on this date 375 years ago: confront the paradoxes presented by nature and find in them, a deeper understanding of Man.